株式投資と一口に言っても、個別株なのかインデックスなのか、またどんなセクターにどのぐらいの分散を効かせて投資するのかなどが人によって異なるため、最適解は各々異なります。
しかし、どのような投資方法であれ不変の要素があります。それは、それぞれの投資対象においてリスクと期待リターンが算出できるということです。
リスクとは投資銘柄の値動き幅の統計値(標準偏差:σ)のことですが、この値を用いることにより最悪のケースを想定した最大下落率を概ね見積もることが可能です。
本記事ではインデックスファンド編として、各人が許容できる損失額と上述のリスクを用いることにより、株式インデックスファンドへの投資額の上限値を簡易的に算出する方法について説明します。
許容損失額から投資上限額を算出する方法

投資上限額を算出するには、まずはじめに許容損失額を決めなければなりません。許容損失額とは、資産運用で損失評価額がここまでなら許せる(耐えられる)というラインのことです。
例えば1000万円投資しているとして、一時的に700万円になるところまでは耐えられそうという場合は、許容損失額は300万円(1000 – 700)となります。
投資銘柄が一つである場合の投資上限額
投資銘柄が一つである場合はとても簡単です。
ここでは例として、S&P500インデックスファンドへの投資を想定します。
S&P500インデックスファンドには様々なものがあるため、ここでは指数自体のパフォーマンスを見てみます。
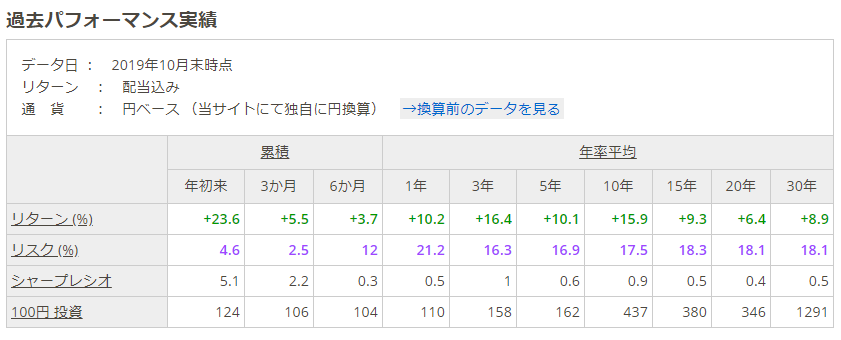
出典:myINDEX
上図は配当込み円ベースでのS&P500の過去のパフォーマンスです。年率平均リスクをみると、この一年間では21.2%ですが、20年と30年では18.1%であることがわかります。
このことから、長期投資では年率18.1%のリスクを見込んでおけば良いですが、損失評価額では短期での変動が重要となるため、ここでは最大値である年率21.2%をS&P500の年間リスクと定めます。
さて、それではS&P500の想定最大損失額を算出しますが、その前に標準偏差についてざっくり解説します。冒頭で述べた通り「リスク=標準偏差(σ)」であり、正規分布という典型的なばらつきの分布を仮定すると、一年後に「平均リターン±σ」の範囲に入る確率が68%である、ということを意味します。
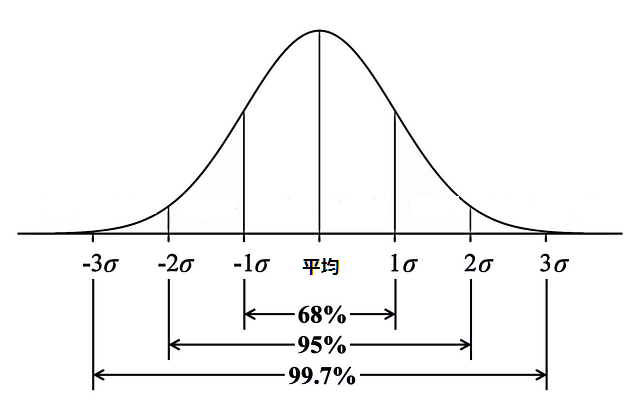
下図は正規分布のグラフを示しております。横軸は値で、縦軸は頻度(または確率)です。
出典:to-kei.net
それでは最大損失幅はいくらかというと、一般的に用いられる指標として最大損失割合は「平均リターン-2σ」とします。平均リターン±2σの範囲に入る確率は95%ですので、これよりもマイナス側になる確率は2.5%です。(プラス側に上振れる確率も2.5%です)
これは、40年間に1回起こるようなケースを仮定していることになり、十分保守的な想定です。なお、リーマンショックは100年に一度という更に悪い結果でしたがそれを見込むのはやりすぎでしょう。
さて、S&P500の直近一年間の平均リターンは10.2%であり、リスク(σ)は21.2%ですので、10.2 – 2×21.2=-32.2%となります。つまり、S&P500であればおおよそ1/3の価値が一年間で失われうると想定しておけばOKです。
今回のケースでは、許容損失額は300万円でしたので、S&P500であれば900万円までなら投資可能であるという結果となります。S&P500の最大損失割合は1/3と求められたので、900万円×1/3=300万円となるからですね。
投資銘柄が複数ある場合の投資上限額
投資銘柄が複数ある場合は、評価方法は複雑になります。
本来は銘柄間の相関係数(どのぐらい値動きに連動性があるか)を算出する必要がありますが、計算が多少複雑になります。
従って、大暴落時では全投資銘柄が一緒に下がるという最悪のケースを想定して「相関係数=1」と保守的に考えて、単純に各銘柄への投資額で重みづけ(加重平均)すればよいと考えられます。
たとえば、TOPIXとS&P500の投資信託にそれぞれ75%と25%投資する場合を考えてみましょう。
TOPIXをmyINDEXで検索すると、直近一年のリスクは16.9%、リターンは3.9%であることがわかります。
出典:myINDEX
従って、95%の確率で収まる±2σの範囲は3.9±2×16.9なので、-29.9%から37.7%となります。つまり、40年に一度の暴落を想定すると、-29.9%の下落率となります。
S&P500での40年に一度の想定下落率は-32.2%でしたから、TOPIX:75%、S&P500:25%のポートフォリオの想定下落率は加重平均により以下のように求まります。
式を言葉にすると以下のように表せます。
上式は銘柄間の相関係数を1と仮定した条件で成り立つ式ですが、インデックス銘柄数が増えた場合も同様に投資割合×想定下落率を足しこんでいけばOKです。
許容損失額は300万円でしたから、300 / 0.305 = 984万円となります。従って、投資上限額は1000万円程度という結果となります。
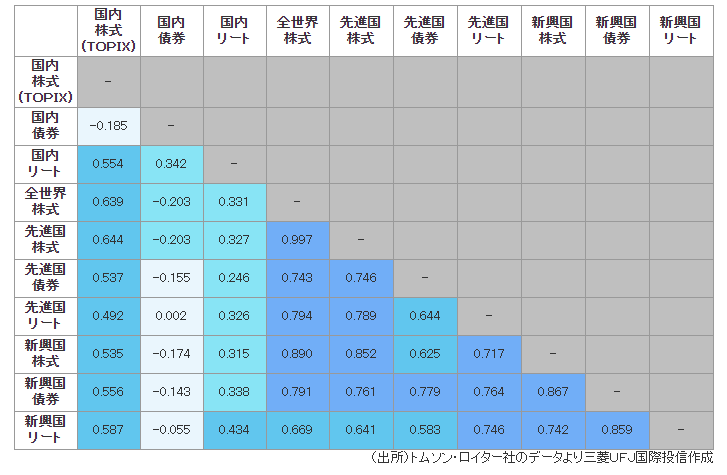
なお、より詳細に下落率を求めたければ、以下の各アセットクラス間での相関係数を用いて評価することもできますが、全アセットクラスが一斉に下落するような最悪のケースを想定する場合は保守的な上記の評価方法(相関係数=1)で十分でしょう。
出典:三菱UFJ国際投信
まとめ
インデックスファンドへの許容損失額から投資可能額を算出する保守的かつ簡易的な方法について説明しました。インデックスファンドであれば期待リターンとリスクが評価されているため、-2σの値を最大下落率と定義して加重平均値を算出すればポートフォリオの最大下落率が算出できます(相関係数=1の条件)。
ここで求めた最大下落率から、許容損失額となるような投資上限額が得られるという算段です。
個別株投資でも、特定の市場に十分に分散している場合は(目安としては20銘柄以上)、その市場のインデックスの期待リターンとリスクを用いて同様の簡易的評価が可能です。
株式市場が高値域にあるうちに投資上限額を算出し、必要であればリバランスを行うことをお勧めします。
以下、関連記事です。
本記事の姉妹記事です。先進国株式市場での年間最大下落幅は、リーマンショック越えの未曽有の大恐慌で1/2と算出できます。

米国株式市場(S&P500)にて長期投資を行う場合の期待リターンの確率分布を、本記事で登場した期待リターンとリスクを用いてモンテカルロシミュレーションという乱数を振る方法(サイコロを沢山振るイメージ)で求めました。

長期的な市場の右肩上がりを想定した積立投資における利回り理論式の導出を以下の記事に示しましたので、理論や数学が好きな方にお楽しみいただければ幸甚です。
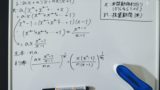



コメント