偉大な物理学者、アインシュタインに「人類史上最大の発明」と言わしめたのは何かご存知でしょうか。
それは複利です。
定期貯金や投資信託等の金融商品においては、利子の扱いを「単利」として分配するか、「複利」として再投資するかのどちらかに設定されています。
物によっては選択可能だったりしますが、「単利」で分配金を得て、そのまま再投資しない場合大きく損をすることとなります。
本記事では、複利によって得られる圧倒的な利益の差を紹介します。
単利と複利の違い
単利と複利の違いを考えてみましょう。
とある年利が10%の金融商品に、100万円預けたとします。
この際、100万円を元本と言いますが、1年目の年利は単利、複利ともに100万円×10%=10万円であり、預金は110万円となります。
(税金は考慮しないものとします)
さて、2年目の預金はどうなるでしょう?
単利の場合:100万円(元本)+10万円(1年目の年利)+10万円(2年目の年利)=120万円
複利の場合:110万円(1円目の年利+元本)+(110万円 × 10%)=110万円 + 11万円=121万円
複利の方が1万円多くなりましたね。
上記のとおり、単利は毎年元本ベースで利率を計算するのに対し、複利は元本に前年の利子を加えた額で利率を考えるのです。
つまり、単利は毎年利子をお金として分配し、複利は毎年利子も含めて再投資しているということですね。
これが単利と複利の違いです。
複利の利益、単利の損失
それでは、単利と複利で利益にどの程度の差があるのか、詳しく見ていきましょう。
計算式
まず、各々のn年後に元本がどうなっているのかを確認する計算式を紹介します。
元本 × (1 + 年利%/100 × n × (1 - 税率%/100))
【複利】
元本 + (元本 × (1 + 年利%/100)^n - 元本) × (1 - 税率%/100)
少しややこしいですが、重要なのはマーカー部です。
単利はn年倍であるのに対し、複利はn年乗になっています。
年数を重ねるにつれ、圧倒的な差が生まれるのが容易に想像できますね。
計算シミュレーション
それでは、前述の計算式を用いて、単利と複利の違いを計算してみましょう。
条件として、元本を100万円、年利を10%、税率は20.315%とします。
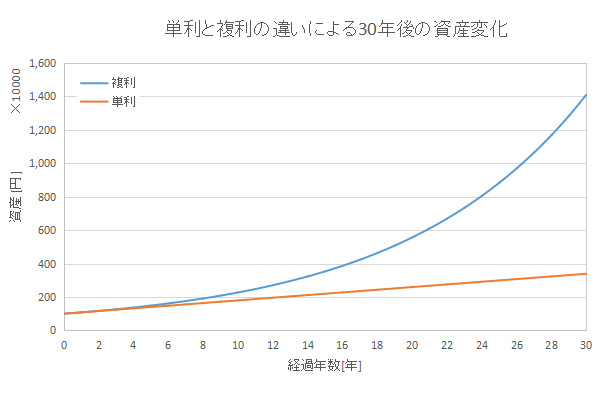
30年後の資産は、単利で339万円、複利で1410万円となりました。
その差はなんと1071万円であり、4.16倍です。
そしてこれは積立投資ではなく、投資額は元本の100万円だけです。
複利と単利ではこんなにも大きな差が出るのです。
当然、さらに年数を重ねたり、積立投資をすると差は広がっていきます。
単利だと実質この差分損ですね。
複利はいわゆる「雪だるま式」というわけです。
例えば、借金の場合は貸す側が複利の恩恵を得るわけですから、借金を返済できずにいると「雪だるま式」に借金が増えていくということですね。
金融商品を選択する際の注意
さて、前節までで複利と単利の圧倒的な違いをご理解いただけたかと思います。
もはや説明不要かと思いますが、金融商品を選択する際は、「再投資型」を選択しましょう。
分配型はダメ、ゼッタイ。
例え分配型だとしても、分配額を再投資するように心掛けましょう。
(分配時の税金分損しますが)
なお、定期預金等、金利が低い(1%未満)金融商品の場合は正直どっちでも良いです。
大して変わりません。定期預金そのものがナンセンスです。
前節の計算条件に対し、定期預金で最高レベルの年利0.3%を適用してみましょう。
・・・30年預金しても350円しか変わりません。
おとなしく再投資型のインデックス投資をしましょう。

まとめ
以上、アインシュタインに人類史上最大の発明と言わしめた(らしい)複利の力の紹介でした。
味方につければこの上なく素敵な効果が得られる反面、敵(借金)に回すと非常に厄介な複利。
金融商品選択の際は必ず「再投資型」にして複利の力を授かりましょう。
そして、借金をする際は利息が単利のプランを選択しましょう(当然、無利息がベストですが)。



コメント